スポットレートとフォワードレートの意味と違い(債券・金利と為替)
記事作成日:2019年7月22日
最終更新日:2021年9月3日
スポットレートとフォワードレートの意味や違いについてです。スポットレートとフォワードレートは債券や金利で使われる場合と外国為替取引で使われる場合で意味が少し異なるため注意が必要です。
債券や金利でのスポットレートは現在から将来のある時点までの金利、フォワードレートは将来のある時点から更に将来のある時点までの金利を意味します。
為替でのスポットレートは今すぐ取引を行う場合の為替レート、フォワードレートは将来のある時点で取引を行う場合の今時点で決めた為替レートを意味します。
スポンサーリンク
債券や金利のスポットレートとは
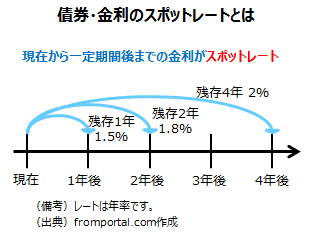
債券や金利でのスポットレート(spot rate)とは、現在から将来のある時点までの金利を意味します。スポットレートは、途中での利払いがなく満期で額面が償還される割引債(ゼロクーポン債)を想定して計算されます。
例えば、現在から1年後までの残存期間が1年の割引債が年率1.5%の利回りとなる場合、1年のスポットレートは1.5%となります。
スポットレートは、将来のお金(将来価値)を現在価値にする割引率として用いられるため、投資や財務などの意思決定や価格計算において重要な意味を持ちます。
金利のスポットレートの計算式・計算方法
現在の価格をA、将来の価格をB、スポットレートをr、満期までの期間(残存期間)をtとし、1年ごとの複利だとすると以下の式が成り立ちます。
A×(1+r)t=B
そのため、スポットレートrは次の通り計算できます。
r=t√(B/A)-1
債券や金利のフォワードレートとは
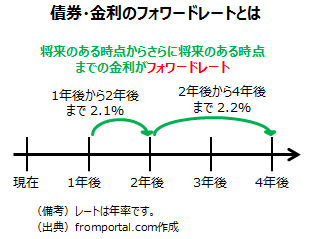
債券や金利でのフォワードレート(forward rate)とは、今の時点での将来のある時点からさらに将来のある時点までの金利を意味します。今の時点から見て、1年後から2年後までの1年間の金利はフォワードレートです。今の時点で計算された将来のレートですが、将来そのレートが実現される保障はありません。現時点で予約した場合の将来の金利という概念です。
フォワードレート(インプライド・フォワードレート)はスポットレートを利用して計算されます。
金利のスポットレートとフォワードレートの違い
金利は現在から将来のある時点までのものがスポットレート、将来のある時点から更に将来のある時点までのものがフォワードレートとなります。金利は基本的にスポットレートかフォワードレートかのどちらかに分類されることになります。
金利のスポットレートとフォワードレートの関係
スポットレートとフォワードレートの間には裁定が働きます。例えば5年間運用する場合に、現在から5年後までの5年のスポットレートで運用する場合と、現在から3年後までの3年のスポットレートと3年後から5年後までの2年間のフォワードレートで運用する場合は同じ結果になるはずなので、有利不利が生じるのであれば裁定機会となり、スポットレートとフォワードレートが変化して調整されます。
金利のフォワードレートの計算方法
現在から将来のある時点までの期間において、どのようなスポットレートとフォワードレートを組み合わせても裁定が働くため同じ運用結果になるという前提を利用してスポットレートからフォワードレートが計算できます。
例えば、現時点から2年後までの2年間運用する場合、現在から2年後までの2年のスポットレートで運用する場合と、現在から1年後までの1年のスポットレートと1年後から2年後までの1年間のフォワードレートを組み合わせて運用する場合は運用結果が同じになるはずです。
金利のフォワードレートの計算式
1年のスポットレートをs1、2年のスポットレートをs2(年率、複利)、1年後から2年後までのフォワードレートをf12とする場合、以下の式が成り立つので、1年と2年のスポットレートからフォワードレートを計算できます。
(1+s2)2=(1+s1)×(1+f12)
一般化すると、a年のスポットレートをsa、b年のスポットレートをsb(年率、複利)、a年後からb年後までのフォワードレートをfabとする場合は、
(1+sb)b=(1+sa)a×(1+fab)(b-a)
となります。上記の式は次の式に変形できます。
fab=(b-a)√((1+sb)b/(1+sa)a)-1
これが金利のフォワードレートの計算式になります。
金利のフォワードレートの計算例
「(1+s2)2=(1+s1)×(1+f12)」の関係式を使って金利のフォワードレートを計算してみます。
残存1年の金利が年1.5%、残存2年の金利が年1.8%の場合、1年後から2年後までのフォワードレートをFとします。残存1年のスポットレート+1年後から2年後までのフォワードレートでの運用と残存2年のスポットレートでの運用結果は等しくなることから、複利計算とすると、(1+1.5%)×(1+F)=(1+1.8%)2となるので、(1.018)2÷(1.015)≒1.021=(1+F)となり、F=2.1%となります。
「fab=(b-a)√((1+sb)b/(1+sa)a)-1」を使う場合、F12=(2-1)√((1+0.018)2/(1+0.015)1)-1=(1.018)2÷(1.015)-1≒0.021となります。
為替のスポットレートとは
外国為替取引でのスポットレート(spot rate)とは、今すぐに実物の取引(現物取引、スポット取引)を行った場合の為替レート(直物為替レート)のことを意味します。為替のスポット取引は基本的に約定の2営業日後に決済(受渡)が行われます(T+2)。スポット(spot)には、「地点」といった意味のほか「その場の、即座の」という意味があります。
例えば、今すぐに1ドル=90円で為替取引を行うことを決めた場合はこの1ドル=90円がスポットレートになります。
為替のスポットレートは、基本的に市場取引の動向を踏まえて決められます。市場取引の場合は市場のレートとなり、相対取引の場合はお互いが合意したレートとなります。
為替のフォワードレートとは
外国為替取引でのフォワードレート(forward rate)とは、将来のある時点であらかじめ決めておいた条件で取引(先物取引(先渡取引)、フォワード取引)を行った場合の為替レート(先物為替レート、予約レート)のことを意味します。フォワード(forward)には、「将来の」や「先の」といった意味があります。
例えば、今、1年後に1ドル=120円で為替取引を行うことを決めた場合はこの1ドル=120円がフォワードレートとなります。
為替のスポットレートとフォワードレートの違い
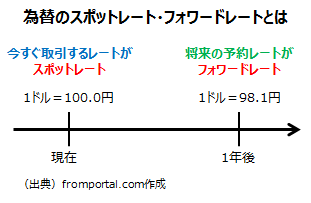
為替でのスポットレートとフォワードレートの違いは、今すぐ取引を行う場合の今のレートがスポットレート(直物為替レート)、今取引の条件を決めるけれど決済は将来行う場合の取引レート(予約レート)がフォワードレート(先物為替レート)ということになります。
スポットレートが基本的に約定の2営業日後に決済(受渡)が行われるため、約定の3営業日以降に決済されるものがフォワード取引となり、その為替レートがフォワードレートとなります。約定の2営業日前に決済されるものがスポット取引でその為替レートがスポットレートになります。
為替のスポットレートとフォワードレートの関係
外国為替のフォワードレートは今現在の為替レート(スポットレート)と、取引完了(決済)までの期間、金利によって決まります。
1年後の為替レートを予約する場合を考えます。外国通貨に交換せずに円のまま保有し円の金利で1年間運用した場合の結果と、今すぐ円を外国通貨にスポットレートで交換して海外の金利で1年間運用しフォワードレートで円に交換した場合の結果が異なる場合は裁定機会となるため、円で保有した場合と外国通貨で保有した場合の運用結果は同じになるようにフォワードレートが決定されます。
為替のフォワードレートの計算方法・計算例
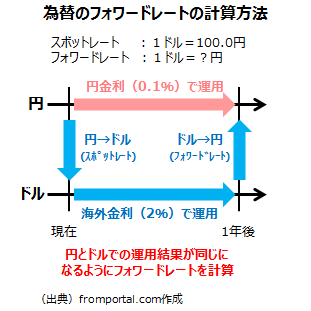
例えば、1年後の決済をするためのフォワードレートを求めるとして、現在の為替レート(スポットレート)が1ドル=100円、日本の金利(円金利)が年0.1%、米国金利が年2.0%の場合を想定して、為替の売買コストを無視して計算します。円で100円を1年間運用すると、100円×(1+0.1%)=100.1円になります。ドルで運用すると100円は1ドルなので、1ドル×(1+2%)=1.02ドルとなります。これをフォワードレートで円に交換すると100.1円になるはずです。そのため、100.1円÷1.02ドル≒98.1円となり、1ドル=98.1円が1年後の予約レート、フォワードレートになります。
為替のフォワードレートの計算式(一般化)
一般化して、初期の運用金額をU円、現在の為替レートを1ドル=S円(ドル以外の海外通貨でも同じです)、フォワードレートを1ドル=F円、円金利を年率ry(小数点表示)、ドルの金利を年率rd(小数点表示)、予約をt年後とすると、円での運用とドルでの運用が等しいことから以下の式が成り立ちます。
U×(1+ry)t=(U÷S)×(1+rd)t×F
この式をFについて解くと以下のようになり、フォワードレートを求めることができます。
F=S×(1+ry)t÷(1+rd)t
まとめ
- 債券や金利のスポットレートは今から将来の特定の時点までの金利、フォワードレートは将来の特定の時点から更に将来までの金利を意味します。
- 為替のスポットレートは今すぐ取引を行う場合の為替レート、フォワードレートは将来取引を行う場合に今の時点であらかじめ決めておく将来の為替レートを意味します。