保険金の期待値は「保険料＋運用益－保険会社の経費や利益等」

記事作成日：2019年3月17日

保険に加入した場合の保険金の期待値は大雑把に１保険契約当たりで「保険料総額＋保険料の運用益－保険会社の経費や利益等」と考えることができます。保険に加入した場合と加入しなかった場合に残るお金の期待値は保険会社の経費や利益などの分だけ、保険に入った方が不利になります。保険は低確率ながら高額の金銭的負担が発生する保険事故に備えて加入すると効果的です。

保険金の期待値は「保険料総額＋保険料の運用益－保険会社の経費と利益」

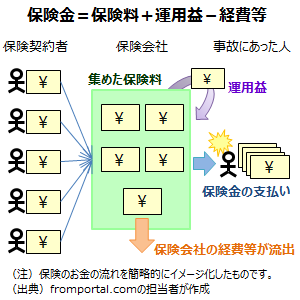
保険では、保険の契約期間中、保険の契約者が保険料を支払い、集められた保険料は国債などにより運用が行われながら、満期時の保険金の支払いも含めた保険事故の支払いに充てられます。ただし、保険会社の経費や利益分が差し引かれていきます。

つまり、集められた保険料の総額に予定利率による一部の保険料の運用益が加わり、保険会社の経費や利益等が差し引かれた残りが契約途中の保険事故の保険金や満期時の保険金の支払いに充てられ、残った分が保険金の期待値となります。

なお、国民年金などの公的保険では税金分の補填があるとその分だけ民間保険より有利になります。

保険金の期待値の具体例

保険金の期待値について具体的な例で考えてみましょう。例えば診断給付金のみがあるがん保険のようなものをイメージします。

仮定する保険の内容

保険の契約期間中に保険事故（がんの診断）が起こると100万円（診断給付金）もらえて、保険事故がないまま満期を迎えた場合にもらえるお金は0円となります。保険事故が起こる確率は契約期間中に50％（2人に1人ががんになる）だとします。

まず、この保険が成立するための保険料は幾らになるかを考えます。集める保険料をどの程度運用するのか、いつ入金するのか、いつ経費等が差し引かれるのかといった技術的な問題はありますが、保険1契約当たり契約期間中に総額10万円の運用益があるとします。また保険会社の経費や利益等として保険1契約当たり契約期間中に総額30万円差し引かれるとします。

想定される保険料の計算

この場合、保険料はいくらなら保険が成立するでしょうか？資金の余裕分や途中脱退など考慮しないとすると、100人が加入した場合に保険事故に備えて集めなければいけない必要な保険料は以下の合計になります（ただし運用益分は控除）。

保険事故の支払いに必要なお金：100人（加入者数）×50％（事故発生確率）×100万円（診断給付金）＝5,000万円（事故の支払いに必要なお金）
保険会社の経費や利益等：100人（加入者数）×30万円（1契約当たりの経費等）＝3,000万円
（控除）保険料の運用益：（-1）×100人（加入者数）×10万円（1契約当たりの運用益）＝▲1,000万円

以上の合計は5,000＋3,000－1,000＝7,000万円であるため、7,000万円÷100人＝70万円が1契約当たりの保険料となります。

保険金の期待値の計算

ここで保険金の期待値は50％の確率で保険事故が発生すると100万円で50％の確率で保険事故が発生しないと0円のため、100万円×50％＋0円×50％＝50万円となります。

つまり、この保険は保険料70万円に対して、保険金の期待値は50万円となります。ここで「保険金の期待値＝保険料＋運用益－経費等」が成り立ち「50万円＝70万円＋10万円－30万円」となります。

保険に入った場合と入らなかった場合に残るお金の期待値の計算

参考として、上記の事例で保険に入った場合と入らなかった場合で保険事故の支払いを行った後にいくら残るかの期待値の計算をします。上記の計算とは、保険金を受け取った後、保険事故に関する支払い（がん保険なら治療費の支払い）を行うという点です。

もらえる保険金と合わせるため、50％の確率で保険事故に遭遇し100万円の支出が発生するとし、50％の確率で保険事故に遭わず支出は発生しないとします。また、保険に入らず浮いた保険料分のお金は保険に入った場合と同じような運用成果になると仮定し、運用益10万円を得られるものとします。

保険に入ると保険料70万円を支払い、保険金の期待値が50万円となりました。保険事故に関する支出の期待値は（▲100万円×50％）＋（0円×50％）＝50万円となるため、保険金の期待値50万円から保険事故の支出の期待値50万円を引くと50万円－50万円＝0円となります。

続いて、保険に入らないと保険料の支払いが浮くため70万円が残ります。浮いたお金で資産運用を行い10万円が得られる一方、保険事故に関する支出の期待値は同様に50万円であるため、保険事故の支出をした後に残るお金は、保険料を支払わず浮いたお金70万円＋運用益10万円－保険事故支出50万円＝30万円となります。

保険に加入すると経費などの分だけ残るお金の期待値が下がる

保険に加入した場合と加入しなかった場合では、保険事故による支出（がんの治療費の支払い等）まで考慮した場合でも、保険会社の経費や利益などの分だけ残るお金の期待値が少なくなります。上記の例では「経費等30万円」の分だけ残るお金に差が出ます。これは保険サービスを受けるために支払うサービス料と考えると分かりやすいかもしれません。

なお、実際には個人と保険会社で同じ運用ができるとは限らないため、運用成績の差も残るお金に反映されます。

保険に加入するかどうかは保険金の期待値と保険事故の発生確率から考える

保険に加入すべきかどうかは、保険料と比較した場合の保険金の期待値と保険事故の発生確率の観点から考えると合理的な判断が出来るようになります。

保険での保険金の期待値

保険に加入した場合の保険金の期待値は、資産運用益が大きいほど高くなり、保険会社の経費や利益等による取り分が大きいほど低くなります。「保険金の期待値＝保険料の支払総額＋資産運用益－保険会社の経費等」であるためです。

保険の資産運用益は予定利率に左右される

資産運用益については保険契約では実際には資産運用の利回りは予定利率で設定され、実際の資産運用益との差は利差益（場合によっては損）となって保険会社の収益に反映されます。予定利率は基本的に保険契約時に決まってしまい、契約中に変更されることは例外を除けばありません。

予定利率は基本的に保険契約時の市場金利の水準に左右されるため、市場金利が低い時は予定利率も低くなっているため、その保険契約の資産運用益はほとんど期待できないということになります。

満期になると保険料より多い保険金がもらえるの保険料が運用されるから

生命保険や学資保険では、契約期間中に死亡などの保険事故が発生しなかった場合でも、満期時に支払った保険料よりも多くの保険金がもらえる仕組みになっていることがあります。保険に入っていたからお金が増えたと思うかもしれませんが、保険に入らなくても増やすことはできます。問題は、保険に入らなかった場合よりも増えるのか、ということです。

保険加入者から集められた保険料は、大雑把に分けると保険事故の発生によって支払われる保険金の部分、保険会社の利益や経費になる部分、将来に備えて資産運用される部分に分かれます。保険会社は集めた保険料で国債などを購入してお金を増やして将来発生する事故の支払いや満期時の支払いなどに備えます。そのため、保険事故が発生しなくても満期時にもらえるお金が増えることがあるのです。

支払った保険料よりも満期に保険金が多くもらえるのは、保険料を資産運用した結果であり、資産運用は保険に加入しなくても自分でできます。実際には、保険会社の経費等が差し引かれるため、同一の運用利回りであれば、期待値の面では保険に入らない方が経費が差し引かれない分だけ通常は高くなります。

保険会社の経費や利益等

保険では集められた保険料から保険を運営するための諸経費と保険会社の利益が差し引かれていきます。保険を運用する仕組みに多くの費用がかかっている場合や保険会社が多くの利益を確保しようとする場合は、多くのお金が差し引かれます。

保険会社の給与水準や販売員が多いなどによって人件費が高い場合、広告宣伝費などに多くのお金をかけている場合、株主への配当が多くなっている場合などは、保険料から多くのお金が差し引かれます。

保険金の期待値は保険会社の経費や利益等のため低くなる

保険での保険金の期待値は保険会社の経費や利益等が差し引かれる分だけ低くなってしまいます。保険を利用するということは予定利率による運用益分によってお金が増える効果が期待できるものの、保険の利用料として保険会社の経費や利益等がかかってしまいます。

資産運用は保険会社と全く同じ状況ではありませんが自分でも行うことができるため、保険に加入しなくても享受することができます。一方で、保険会社の経費や利益等は保険を利用しなければ発生しません。そのため、保険を使わなくていいのであればできる限り使わないということが期待値の面では正しいのです。

保険事故の発生確率

期待値の面では保険を利用しない方が保険会社の経費や利益等に相当するお金が失われないため合理的ということになります。しかし、保険は必要です。なぜ必要かと言えば、保険事故が発生した場合に確率的に大きな金銭負担を負うことがあるため、保険によってリスクを減らすことが経済的に合理的であるからです。

保険会社の経費等を除けば「保険金＝保険料÷発生確率」になる

例えば診断給付金のみがあるがん保険のようなものをイメージします。保険の契約期間中に保険事故（がんの診断）が起こると100万円（診断給付金）もらえて、保険事故がないまま満期を迎えた場合にもらえるお金は0円となります。保険事故が起こる確率は契約期間中に50％（2人に1人ががんになる）だとします。この場合保険料はいくらなら保険が成立するでしょうか？

資金の余裕分と保険会社による事務の経費や利益、運用による増加分、途中脱退などは一切発生しないとすると、100人が加入した場合に保険事故に備えて集めなければいけない必要な保険料は100人（加入者数）×50％（事故発生確率）×100万円（診断給付金）＝5,000万円（事故の支払いに必要なお金）となります。

5,000万円を加入者100で分けるのですから、5,000万円÷100人＝50万円／人が加入者がこの保険で支払う保険料となります。この場合、保険料（50万円）はもらえる保険金100万円×発生確率50％となっていて、「保険料＝保険金×発生確率」となっていて、式を変形すると、「保険金＝保険料÷発生確率」となり、もらえる保険金は保険料を発生確率（50％＝1/2）の逆数を掛けたもの（×2）となっています。

発生確率が高い保険事故では保険金が少なくなる

保険は発生確率が高い保険事故の場合、それほど多くの保険金がもらえるわけではないのです。そのため、保険が発生しない可能性や実際には保険会社の経費や利益がかかること、保険金は保険事故が発生しないともらえず資金使途に制約があることを考えると、誰もが直面する可能性が高い保険事故は保険ではなく、自分で備えた方が良いこともあるのです。

反対に保険事故に遭った場合に高額の金銭的負担が発生するような場合、保険に加入することで金銭的なリスクを抑えることができるようになります。

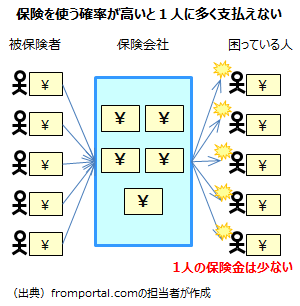
例えば、保険事故の確率が高い場合、保険金を支払う人が増えるため1人当たりの保険金は少なくなります。集めた保険金をより多くの人で分けるため、1人当たりの取り分は少なくなるわけです。

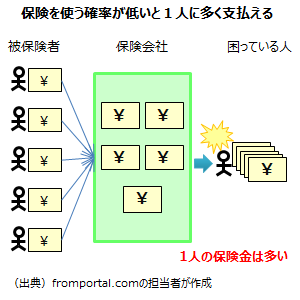
逆に保険事故の確率が低い場合、保険金を全くもらえない人あるいは少ししかもらえない人が多く出ますが、集めた保険金を少ない人で分けるため、1人当たりの取り分、保険金は多くなります。

なぜ保険に入るのか？

では、保険に入ると入らなかった場合と比べてもらえるお金の期待値が低くなるのになぜ保険に入る必要があるのでしょうか。それは確率が低いものの発生すると通常では支払えないようなお金の負担が発生する場合があるためです。

保険金の期待値が保険に入らなかった場合に残るお金の期待値よりも低いのであれば、経済的な判断としては保険に入らない方が得です。しかし、実際には保険事故に遭遇すると低い確率で数千万円といった金銭的負担が発生するリスクがあり、このリスクに遭遇しても困らないために保険に入るのです。

つまり、発生確率が低く、多額の金銭的な負担が発生する可能性がある保険事故に備えて、金銭的なリスク管理のために保険に入るのです。

保険に加入する意義と入るべき保険

保険に加入する意義は、発生確率が低くかつ金銭的負担が大きいリスクに金銭的に備えられることです。

例えば自動車事故における損害賠償責任を負うと、数千万円、1億円を超える金銭的な負担が発生する可能性があります。また、火災や地震などによる自宅の損傷（火災保険、地震保険）、日常事故による損害賠償（個人賠償責任保険）、働き盛りの時期における病気やけがによる死亡（生命保険）や就業不能（所得補償保険）、病気における一部の先進医療等の医療費（医療保険やがん保険などの先進医療特約）では高額の金銭的負担が発生する可能性があります。このような場合には、保険に加入する意義があるのです。

なお、保険は安全・安心のためといったことが言われますが、保険加入と保険事故が発生する確率は基本的に無関係なので、保険事故を減らす効果はないため安全にはつながりません。そのため、保険に加入すると「安心」なのです。

ただし、保険に入ると金銭的な備えができていない場合は保険金で保険事故後の生活が保障される（＝衣食住を確保＝安全）ため、安全であると言えます。金銭的な備え、貯金が少ない人も保険に入ることが望ましい場合が多いのです。

まとめ

保険に加入した場合の保険金の期待値は「支払った保険料の総額＋保険料の運用益－保険会社の経費や利益等」となります。
保険に加入した場合と加入しなかった場合に残るお金の期待値は保険会社の経費や利益などの分だけ、保険に入った方が不利になります。