現価係数とは(意味や定義・使い方・計算式・現価係数表)
記事作成日:2018年4月13日
現価係数とは、一定期間、一定利率で複利運用した後で一定の金額にするためには、現在いくら必要になるかを計算するために使う係数です。現価係数の定義は「将来の金額×現価係数=現在の金額」から、「現価係数=現在の金額÷将来の金額」となります。つまり現価係数とは、現在の金額は将来の金額の何倍(利率がプラスの場合、1倍未満)になるのかを示した係数です。将来の金額に現価係数をかけることで現在必要となる金額が分かります。
「現価係数」の読み方は「げんかけいすう」です。現価係数の英語は「present value factor」、「present worth factor」などとなります。異なる表現をしている場合があるため注意が必要です。
また、「終価係数=将来の金額÷現在の金額」であることから、現価係数は終価係数の逆数です。
スポンサーリンク
現価係数の図解
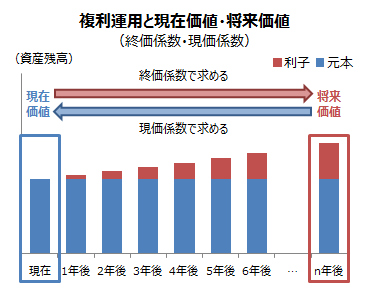
現価係数とは、複利運用した場合に将来の金額(元利金)から現在の金額(元本・原資)を求める係数です。将来の金額(将来価値)に現価係数をかけることで現在の金額(現在価値)を求めることができます。現価係数の場合は、途中で積み立てなどは行われず、期間中は複利運用が行われます。
現価係数の使い方・使用例
現価係数は「将来の金額×現価係数=現在の金額」となるため、将来の金額に現価係数をかけると現在必要となる金額や現在価値を求めることができます。
複利運用の途中に元本の追加などを行わない場合に、将来必要な金額を得るために、現在いくら原資が必要かを計算するために用いられます。また、現価係数は現在価値を求める場合に用いられます。
現価係数は現在価値を求めるために使う
現価係数は将来の価値(金額)から現在の価値(金額)を求める場合も用いられます。時点が異なる2つの価値(金額)は単純に比較できないので、同じ一時点の金額に割り引いて比較をします。
よくある例が、今すぐもらえる100万円と、将来もらえる100万円のどちらの価値が高いかというような場合です。
将来までの期間、将来までの利率での現価係数が0.9000だったとすると、今すぐもらえる現在の100万円と将来もらえる100万円を現在にそろえて比較すると、現在の100万円は修正の必要がなく、将来の100万円は100×0.9000=90(万円)となるため、現在の100万円(現在価値:100万円)と将来の100万円(現在価値:90万円)では現在の100万円の方が良いということになります。
利率がプラスの場合、現在から将来に向かって複利運用をすれば必ず資産は増えていきます。逆にいうと将来の価値を現在の価値に直す場合は、利率がプラスであれば必ず金額は減少します。将来の金額(価値)×現価係数=現在の金額(価値)なので、現価係数は利率がプラスなら必ず1よりも小さい値となります。
正味現在価値法と現価係数
正味現在価値法(NPV法)では、ディスカウント(割引)キャッシュフロー法(DCF法)の考え方に基づいて現在から将来までのキャッシュフローをすべて現在価値に割り戻して、現在価値の総額がプラスであれば投資を行うという投資の意思決定の方法です。この場合の利率を割引率などといいますが、企業の資金調達コスト(資金調達の利率)である資本コストを用いる場合があります。
各年のキャッシュフローに対して現価係数を掛けることで現在価値が算出できるため、現価係数の概念を知っていると計算を効率的に行える場合があります。
インフレ(物価上昇)による実質的な貨幣価値の減少の計算
最初100円であった商品が、一定期間経過後150円になったとします。最初300円を持っていたとすると、商品は3個購入できます(300÷100=3)。しかし、一定期間経過後は2個しか購入できません(300÷150=2)。
この商品に限ってみれば、300円は最初商品3個分の価値があったのに、一定期間経過後は2個分の価値に低下してしまいました。300円は、2÷3≒0.667=66.7%の価値に実質的に減少したのです。
「実質金額÷名目金額」によって実質値は名目値の何割(何%)まで価値が減少したのかを計算することができます。「名目金額÷物価上昇率=実質金額」であることから、「実質金額÷名目金額=1÷物価上昇率」となります。
この時、一定期間、一定の利率で複利計算を行い将来の値を計算するのは終価係数であるため同じ条件の場合の物価上昇率に置き換えて利用することができ、現価係数と終価係数は逆数の関係にあることから、「1÷物価上昇率」=「1÷終価係数」=「現価係数」となります。
現価係数は、インフレ(物価上昇)による実質的な貨幣価値の減少程度を知ることができるのです。
現価係数の例題
(例題1)年率1%で複利運用して10年後に100万円にする場合に今必要な元本はいくらか?
利率1%、10年の現価係数は0.9053なので、100×0.9053=90.53(万円)となります。
(例題2)割引率を2%とすると、10年後の100万円の現在価値はいくらか?
利率2%、10年の現価係数は0.8203なので、100×0.8203=82.03(万円)となります。
(例題3)毎年2%の物価上昇が10年間続いた場合、現在の100万円は将来の時点で実質的な購買力は現在の何倍になるか?
「実質金額÷名目金額」=「1÷物価上昇率」であり、物価上昇率は終価係数によって求められますが、「1÷終価係数=現価係数」のため、利率2%、10年の現価係数は0.8203なので、0.8203倍になります。
現価係数の求め方・出し方
現価係数は現価係数表がある場合には、現価係数表から現価係数の値を探して求めます。現価係数表がない場合には、現価係数の計算式から現価係数を自分で計算によって算出する方法によって求めます。
現価係数を計算で算出する方法(計算式)
現価係数は現価係数表がある場合には現価係数表から値を求めます。現価係数表がない場合、現価係数表には載っていない場合には、次の現価係数の計算式から計算で求める方法もあります。現価係数の出し方は次の計算式に「r:利率(年間の運用利率)」と「n:期間(年)」を入力することによって算出することができます。
現価係数:1/(1+r)n
現価係数の計算式の求め方
現価係数は希望する将来の金額にするために、一定期間、一定利率で複利運用する場合に必要な現在の金額(原資)を求める係数です。
「r」を年間の運用利率、「n」を運用年数とすると、n年後、n-1年後、・・・・n-(n-1)年後(1年後)、n-n年後(0年後)の値の式から、現価係数を次のように求めることができます。
ここで「Fn」を期間n年の現価係数、「An」をn年後の金額、「A0」を現在必要な金額とします。なお、現価係数は終価係数の逆数であるため、終価係数の逆数としても求めることができます。
現価係数の定義から次の関係が成り立ちます。
An・Fn=A0…(1)
n年後の金額(An)はn-1年後の金額を(1+r)倍しているため、n-1年後の金額を求めるにはn年後の金額を(1+r)で割ればよいことになります。
n-1年後:An-1=An/(1+r)
以下同様に立式できます。
n-2年後:An-2=An-1/(1+r)
n-3年後:An-3=An-2/(1+r)
以上から、次々と(1+r)で割っていくことが確認できます。n-n=0から次の式が成り立ちます。
n-n年後(0年後):An-n=A0=An-(n-1)/(1+r)
以上より、n回分(1+r)で割っていることから、0年後は次の通りとなります。
0年後:A0=An/(1+r)n…(2)
(1)と(2)から次の関係を導くことができます。
Fn=1/(1+r)n
現価係数の覚え方
将来の金額から現在の金額を求めるので現価係数となります。現価係数に似た言葉で年金現価係数がありますが、この年金という言葉は毎年の金額(を受け取る)の意味です。将来の金額から現在の金額を求める場合には、毎年原資を追加したり、原資を取り崩したりする操作がないので、年金という言葉は必要ないことになります。
現価係数と年金現価係数の違いは、現価係数は原資の追加や取崩がない時に将来の金額から現在必要な金額を求める一方、年金現価係数は毎年受け取る年金額から現在必要な金額を求めるという違いがあります。
現価ということで現在の金額を求めるということ、年金という言葉ないため、毎年の原資の追加や取崩がないことを理解しておくと覚えやすくなります。
現価係数を計算するエクセル関数
現価係数をエクセルで計算する場合には、PV関数を用います。PVは「Present Value」(現在価値)です。PV関数は(利率,期間,定期支払額,将来価値,支払期日)を入力します。
終価係数を計算したい場合、利率には複利運用する利率(例:1%なら0.01または1%)、期間には運用期間(例:5年なら5)、定期支払額は「0」(積立等はありません)、将来価値は「-1」(負の結果となるためマイナスとし、将来価値が1になると設定)、支払期日は省略するか「0」(通常期末で算出します)と入力します。
現価係数表
現価係数表は以下の通りとなります。複利運用の場合に必要な元本を計算するための表としても使えます。
| 期間 | 1% | 2% | 3% | 4% | 5% |
|---|---|---|---|---|---|
| 1 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 |
| 2 | 0.9803 | 0.9612 | 0.9426 | 0.9246 | 0.9070 |
| 3 | 0.9706 | 0.9423 | 0.9151 | 0.8890 | 0.8638 |
| 4 | 0.9610 | 0.9238 | 0.8885 | 0.8548 | 0.8227 |
| 5 | 0.9515 | 0.9057 | 0.8626 | 0.8219 | 0.7835 |
| 6 | 0.9420 | 0.8880 | 0.8375 | 0.7903 | 0.7462 |
| 7 | 0.9327 | 0.8706 | 0.8131 | 0.7599 | 0.7107 |
| 8 | 0.9235 | 0.8535 | 0.7894 | 0.7307 | 0.6768 |
| 9 | 0.9143 | 0.8368 | 0.7664 | 0.7026 | 0.6446 |
| 10 | 0.9053 | 0.8203 | 0.7441 | 0.6756 | 0.6139 |
| 11 | 0.8963 | 0.8043 | 0.7224 | 0.6496 | 0.5847 |
| 12 | 0.8874 | 0.7885 | 0.7014 | 0.6246 | 0.5568 |
| 13 | 0.8787 | 0.7730 | 0.6810 | 0.6006 | 0.5303 |
| 14 | 0.8700 | 0.7579 | 0.6611 | 0.5775 | 0.5051 |
| 15 | 0.8613 | 0.7430 | 0.6419 | 0.5553 | 0.4810 |
| 16 | 0.8528 | 0.7284 | 0.6232 | 0.5339 | 0.4581 |
| 17 | 0.8444 | 0.7142 | 0.6050 | 0.5134 | 0.4363 |
| 18 | 0.8360 | 0.7002 | 0.5874 | 0.4936 | 0.4155 |
| 19 | 0.8277 | 0.6864 | 0.5703 | 0.4746 | 0.3957 |
| 20 | 0.8195 | 0.6730 | 0.5537 | 0.4564 | 0.3769 |
| 21 | 0.8114 | 0.6598 | 0.5375 | 0.4388 | 0.3589 |
| 22 | 0.8034 | 0.6468 | 0.5219 | 0.4220 | 0.3418 |
| 23 | 0.7954 | 0.6342 | 0.5067 | 0.4057 | 0.3256 |
| 24 | 0.7876 | 0.6217 | 0.4919 | 0.3901 | 0.3101 |
| 25 | 0.7798 | 0.6095 | 0.4776 | 0.3751 | 0.2953 |
| 26 | 0.7720 | 0.5976 | 0.4637 | 0.3607 | 0.2812 |
| 27 | 0.7644 | 0.5859 | 0.4502 | 0.3468 | 0.2678 |
| 28 | 0.7568 | 0.5744 | 0.4371 | 0.3335 | 0.2551 |
| 29 | 0.7493 | 0.5631 | 0.4243 | 0.3207 | 0.2429 |
| 30 | 0.7419 | 0.5521 | 0.4120 | 0.3083 | 0.2314 |
| 31 | 0.7346 | 0.5412 | 0.4000 | 0.2965 | 0.2204 |
| 32 | 0.7273 | 0.5306 | 0.3883 | 0.2851 | 0.2099 |
| 33 | 0.7201 | 0.5202 | 0.3770 | 0.2741 | 0.1999 |
| 34 | 0.7130 | 0.5100 | 0.3660 | 0.2636 | 0.1904 |
| 35 | 0.7059 | 0.5000 | 0.3554 | 0.2534 | 0.1813 |
| 36 | 0.6989 | 0.4902 | 0.3450 | 0.2437 | 0.1727 |
| 37 | 0.6920 | 0.4806 | 0.3350 | 0.2343 | 0.1644 |
| 38 | 0.6852 | 0.4712 | 0.3252 | 0.2253 | 0.1566 |
| 39 | 0.6784 | 0.4619 | 0.3158 | 0.2166 | 0.1491 |
| 40 | 0.6717 | 0.4529 | 0.3066 | 0.2083 | 0.1420 |
(注)期末に利子の処理を行う方式、小数第5位を四捨五入。
(出典)fromportal.comの担当者が作成
まとめ
- 現価係数は、一定期間、一定利率で複利運用する場合に将来の一定の金額を得るためには、現在いくら必要になるかを計算するために使う係数です。
- 将来の金額に現価係数をかけることで現在必要な金額(原資)を求めることができます。