FPがライフプランで使う複利計算の6つの係数の違いと覚え方
記事作成日:2018年4月27日
複利計算で用いる終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数の6つの係数があります。単利であれば、元本×金利×期間で利息を簡単に計算することができるため、複数年の運用結果も容易に算出できます。しかし、複利の場合は利息に対しても利息が発生するため、複数年の運用結果の計算は複雑になります。
様々な金利、期間で複利運用を行った場合にどうなるかを簡単に計算するために終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数の6つの係数が役に立ち、ライフプランを作成する際にファイナンシャルプランナー(FP)が良く用います。
スポンサーリンク
6つの係数の特徴・意味・使い方
複利計算に使う6つの係数は次の6つで、基本的な意味はそれぞれ下記の通りになります。
終価係数の特徴・意味・使い方
終価係数とは、現在の元本を一定期間、一定利率で複利運用すると、将来いくらになるかを計算するために使う係数です。「最初の元本金額(現価)×終価係数=運用後の金額(終価)」というように使います。
現価係数の特徴・意味・使い方
現価係数とは、一定期間、一定利率で複利運用した後で一定の金額にするためには、現在いくら必要になるかを計算するために使う係数です。「運用後の金額(終価)×現価係数=最初の元本金額(現価)」というように使います。
年金終価係数の特徴・意味・使い方
年金終価係数とは、一定の期間、一定の金額を毎期同額で積み立てながら、一定の利率で複利運用した場合、将来いくらになるかを計算するための係数です。「毎年出入りする金額(積立金)×年金終価係数=運用後の金額(終価)」というように使います。
減債基金係数の特徴・意味・使い方
減債基金係数とは、将来目標となる金額を貯めるために、一定の期間、一定の利率で複利運用する場合、毎期いくらの金額を積み立てればよいかを計算するための係数です。「運用後の金額(終価)×減債基金係数=毎年出入りする金額(積立金)」というように使います。
年金現価係数の特徴・意味・使い方
年金現価係数とは、将来の一定期間、毎期同額の希望する年金額を受け取る場合に必要となる現在時点での元本(年金原資)はいくらになるかを計算するために使う係数です。なお、元本は一定利率で複利運用します。「毎年出入りする金額(取崩金)×年金現価係数=最初の元本金額(現価)」というように使います。
資本回収係数の特徴・意味・使い方
資本回収係数とは、現在の元本を一定期間、一定利率で複利運用しながら、毎期同額ずつ取り崩す(回収する、受け取る)場合に毎期の取崩金額(回収金額、受取金額)はいくらになるかを計算するために使う係数です。「最初の元本金額(現価)×資本回収係数=毎年出入りする金額(取崩金」というように使います。
6つの係数の基本的なルール・理解の仕方
終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数の6つの係数は名前や何を求めるために使うのかが難解で非常に理解しづらい、覚えづらいものです。しかし、特徴を理解すれば6つの係数を覚えやすくなります。 6つの係数の覚え方・理解の仕方のポイントは次の通りです。
6つの係数の基本的なルール
- 運用年数と運用年利を決めると具体的な係数の値が決まる
- 運用方法には「元本のみ運用(元本運用)」、「積み立てながら運用(積立運用)」、「取り崩しながら運用(取崩運用)」の3つがある
- 係数で求める値には、「最初の元本金額(現価)」、「運用後の金額(元利金)(終価)」、「毎年出入りする金額(積立金または取崩金)」(厳密には毎年は年に限らず「毎期」)の3つがある
- 積立運用の最初の元本金額は0、運用後の金額は0ではない
- 取崩運用の運用後の金額は0、最初の元本金額は0ではない
元本運用
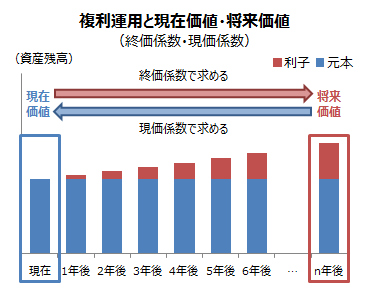
元本運用は最初の元本のみを運用して、途中でお金を引き出したり(取崩)、積み立てたり(積立)はありません。求める対象となるの「最初の元本金額(現価)」か「運用後の金額(終価)」です。
- 最初の元本金額(現価):現価係数
- 運用後の金額(終価):終価係数
積立運用
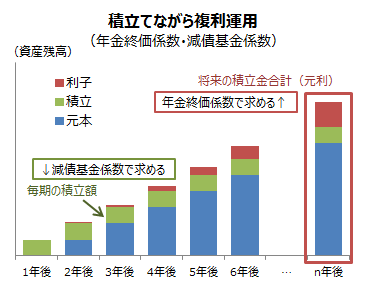
積立運用は途中でお金を積み立てながら運用します(通常は各期末(年末)に積立金を追加)。ただし、積み立てる前の最初の元本金額(現価)は0という設定です。求める対象となるのが「毎年出入りする金額(積立金額)」か「運用後の金額(終価)」です。最初の元本金額(現価)は0なので求める対象とはなりません。
- 毎年出入りする金額(積立金額):減債基金係数
- 運用後の金額(終価):年金終価係数
取崩運用
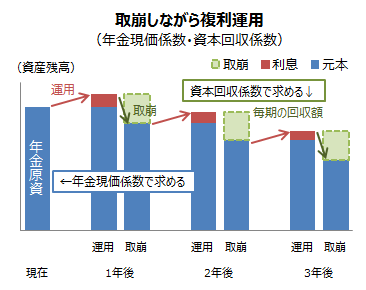
取崩運用は途中でお金を取崩ながら運用します(通常は各期末(年末)に取崩金を引き出し)。ただし、取り崩したお金は最終的になくなるため、運用後の金額(終価)は0という設定です。求める対象となるのが「毎年出入りする金額(取崩金額)」か「最初の元本金額(現価)」です。運用後の金額(終価)は0なので求める対象とはなりません。
- 毎年出入りする金額(取崩金額):資本回収係数
- 最初の元本金額(現価):年金現価係数
複利運用の6つの係数で求めるもののまとめ
| 係数 | 運用形態 | 求めるもの | 既知のもの |
|---|---|---|---|
| 終価係数 | 元本運用 | 終価 | 現価 |
| 現価係数 | 元本運用 | 現価 | 終価 |
| 年金終価係数 | 積立運用 | 終価 | 毎期の金額(積立金) |
| 減債基金係数 | 積立運用 | 毎期の金額(積立金) | 終価 |
| 年金現価係数 | 取崩運用 | 現価 | 毎期の金額(取崩金) |
| 資本回収係数 | 取崩運用 | 毎期の金額(取崩金) | 現価 |
(出典)fromportal.comの担当者が作成
6つの係数の計算式
終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数を運用年数と運用年利から計算する式は次の通りとなります。nが運用年数(運用期間)、rが運用年利率(運用期間の利率)です。
| 係数 | 計算式 |
|---|---|
| 終価係数 | (1+r)n |
| 現価係数 | 1/(1+r)n |
| 年金終価係数 | {(1+r)n-1}/r |
| 減債基金係数 | r/{(1+r)n-1} |
| 年金現価係数 | {(1+r)n-1}/{r・(1+r)n} |
| 資本回収係数 | {r・(1+r)n}/{(1+r)n-1} |
(出典)fromportal.comの担当者が作成
6つの係数のエクセルでの計算式
6つの係数をエクセルで計算する場合は次の関数式を用います。
| 係数 | エクセル関数 |
|---|---|
| 終価係数 | FV(年利率,年数,0,-1,0) |
| 現価係数 | PV(年利率,年数,0,-1,0) |
| 年金終価係数 | FV(年利率,年数,-1,0,0) |
| 減債基金係数 | PMT(年利率,年数,0,-1,0) |
| 年金現価係数 | PV(年利率,年数,-1,0,0) |
| 資本回収係数 | PMT(年利率,年数,-1,0,0) |
(出典)fromportal.comの担当者が作成
6つの係数の覚え方
終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数は何を求めるために使うのかの覚え方は次の通りです。
終価係数と現価係数の覚え方
- 「現価」とつく場合は最初の元本金額(現価)を求めるために使う
- 「終価」とつく場合は運用後の金額(終価)を求めるために使う
- 文字数が少ない係数(終価係数、現価係数)は単純な元本のみ運用の計算に使う
年金終価係数と年金現価係数の覚え方
- 「現価」とつく場合は最初の元本金額(現価)を求めるために使う
- 「終価」とつく場合は運用後の金額(終価)を求めるために使う
- 「年金」という言葉は毎年出入りする金額(年金:積立金または取崩金)を意味し、積立運用か取崩運用のどちらかに関係する
- 「年金」がつく係数(年金終価係数、年金現価係数)は毎年出入りする金額(年金:積立金または取崩金)が分かっている場合や与えられている場合に使うのであって、毎年出入りする金額(年金:積立金または取崩金)を求めるために使うのではない
- 年金終価係数は、「終価」とつくため運用後の金額(終価)を求める(=0ではない)ため、最初の元本金額は0となり、積立運用で終価を求めるために使う
- 年金現価係数は、「現価」とつくため最初の元本金額(現価)を求める(=0ではない)ため、運用後の金額(終価)は0となり、取崩運用で現価を求めるために使う
減債基金係数と資本回収係数の覚え方
- 6つの係数のうち、終価係数、現価係数、年金終価係数、年金現価係数は毎年出入りするお金(年金:積立金または取崩金)を求めるために使うのではないため、減債基金係数と資本回収係数が毎年出入りする金額(年金:積立金または取崩金)を求めるために使う
- 元本運用以外で「年金」が付かない場合は毎年出入りする金額(年金:積立金または取崩金)を求めるために使う
- 「減債基金」とは将来債務を返済(減債)するために定期的に積み立てる基金という意味であることを覚え、連想で減債基金係数は定期的な「積立金額」を求めるために使うと理解する
- 資本回収係数は「回収」という言葉から定期的な「取崩金額」を計算するために使うと連想する
6つの係数の覚え方のまとめ
| 係数 | 覚え方 |
|---|---|
| 終価係数 | 「終価」しかつかないため単純な元本運用で「終価」を求める |
| 現価係数 | 「現価」しかつかないため単純な元本運用で「現価」を求める |
| 年金終価係数 | 「年金」(≒毎年お金が出入り)で「終価」が付くため積立運用(終価≠0)で「終価」を求める |
| 減債基金係数 | 「減債基金」はお金の積立を意味し「年金」が付かないので「毎期の積立金」を求める |
| 年金現価係数 | 「年金」(≒毎年お金が出入り)で「現価」が付くため取崩運用(現価≠0)で「現価」を求める |
| 資本回収係数 | 「資本回収」はお金の取崩を意味し「年金」が付かないので「毎期の取崩金」を求める |
(出典)fromportal.comの担当者が作成
6つの係数と運用年数・運用年利率の関係
6つの係数と運用年数・運用年利率の関係は次のようになります。
| 係数 | 係数(a)の値 | 運用年数が増えると係数は | 運用年利が高くなると係数は |
|---|---|---|---|
| 終価係数 | a>1 | 大きくなる | 大きくなる |
| 現価係数 | a<1 | 小さくなる | 小さくなる |
| 年金終価係数 | a≧1 1年の係数は1 | 大きくなる | 大きくなる(1年を除く) |
| 減債基金係数 | a≦1 1年の係数は1 | 小さくなる | 小さくなる(1年を除く) |
| 年金現価係数 | a>0 1年の係数は1未満 | 大きくなる | 小さくなる |
| 資本回収係数 | a>0 1年の係数は1超 | 小さくなる | 大きくなる |
(出典)fromportal.comの担当者が作成
終価係数と運用年数・運用年利率の関係
終価係数は元本運用で運用後の金額(終価)を求めるために使います。運用年数が大きいほど運用後の金額は増えるため、終価係数は大きくなります。運用年利が高くなると運用後の金額は増えるため、終価係数は大きくなります。
現価係数と運用年数・運用年利率の関係
現価係数は元本運用で必要となる最初の元本金額(現価)を求めるために使います。運用年数が大きいほど運用で増えることから元本は少なくて済み、現価係数は小さくなります。運用年利が高くなると運用で増えることから元本は少なくて済み、現価係数は小さくなります。
年金終価係数と運用年数・運用年利率の関係
年金終価係数は積立運用で運用後の金額(終価)を求めるために使います。運用年数が大きいほど運用後の金額は増えるため、年金終価係数は大きくなります。運用年利が高くなると運用後の金額は増えるため、年金終価係数は大きくなります。
減債基金係数と運用年数・運用年利率の関係
減債基金係数は積立運用で必要な運用後の金額が決まっている場合に、毎期出入りする金額(積立金)を求めるために使います。運用年数が大きいほど運用で増えることから毎期の積立金は少なくて済み、減債基金係数は小さくなります。運用年利が高くなると運用で増えることから毎期の積立金は少なくて済み、減債基金係数は小さくなります。
年金現価係数と運用年数・運用年利率の関係
年金現価係数は取崩運用で最初の元本金額(現価)を求めるために使います。運用年数が大きいほど取崩に備えて必要な元本金額は増えるため年金現価係数は大きくなります。運用年利が高くなると運用で増えるため必要な元本金額は少なくて済み、年金現価係数は小さくなります。
資本回収係数と運用年数・運用年利率の関係
資本回収係数は取崩運用で最初の元本金額が決まっている場合に、毎期出入りする金額(取崩金)を求めるために使います。運用年数が大きいほど各期に取崩ができる金額は少なくなるため資本回収係数は小さくなります。運用年利が高くなると運用で増えるため毎期取崩できる金額は多くなり、資本回収係数は大きくなります。
まとめ
- 終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数は複利運用を行った場合に「最初の元本金額(現価)」、「運用後の金額(元利金)(終価)」、「毎年出入りする金額(積立金または取崩金)」を求めるために使います。
- 終価係数、現価係数、年金終価係数、減債基金係数、年金現価係数、資本回収係数は複利運用では「元本のみ運用(元本運用)」、「積み立てながら運用(積立運用)」、「取り崩しながら運用(取崩運用)」の3つがあることに注意が必要です。