年金現価係数とは(意味や定義・使い方・計算式・年金現価係数表)
記事作成日:2018年4月14日
年金現価係数とは、将来の一定期間、毎期同額の希望する年金額を受け取る場合に必要となる現在時点での元本(年金原資)はいくらになるかを計算するために使う係数です。なお、元本は一定利率で複利運用します。
年金現価係数の定義は「毎期(毎年)の受取金額×年金現価係数=現在の元本金額(年金原資)」から、「年金現価係数=現在の元本金額(年金原資)÷毎期(毎年)の受取金額」となります。
つまり、年金現価係数とは、毎期(毎年)の受取金額(年金)の何倍年金原資が必要なのかを示した係数です。毎期の受取金額に年金現価係数をかけることで、現在必要な年金原資(元本)が分かります。
「年金現価係数」の読み方は「ねんきんげんかけいすう」です。年金現価係数は複利年金現価率(ふくりねんきんげんかりつ)と呼ぶこともあります。年金現価係数の英語は「uniform series present worth factor」などとなります。
また、「資本回収係数=毎期の取崩金額÷現在の元本金額」であることから、年金現価係数は資本回収係数の逆数です。
スポンサーリンク
年金現価係数の図解
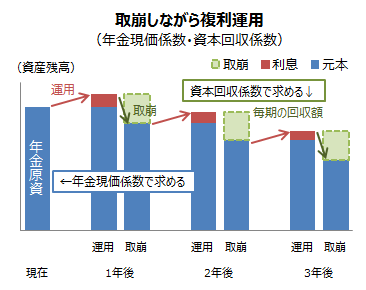
年金現価係数とは、現在の元本(年金原資)を毎期一定金額取崩しながら、一定期間、一定利率で複利運用した場合に、必要となる現在の元本金額(年金原資)を求める係数です。希望する毎期の取崩金額に年金現価係数をかけることで必要となる現在の元本金額(年金原資)を算出できます。
年金現価係数の使い方・使用例
年金現価係数は「毎期(毎年)の受取金額×年金現価係数=現在の元本金額(年金原資)」となるため、希望する毎期(通常は年単位で毎年)の受取金額に年金現価係数をかけると、現在必要な元本金額(年金原資)を求めることができます。相続などの場面において、将来一定金額の収入が発生する資産の現在価値を計算するためにも用いられることがあります。
将来希望する年金額を受け取るために必要な年金原資(退職金、貯金、老後資金)を求める場合に使用されます。また、住宅ローンなどの借入金の毎年の返済金額が決まっている場合に借入金総額を求める場合にも利用できます。
ただし、住宅ローンなど返済は通常1年に1回期末だけという訳ではなく毎月行われるため、年単位で年金現価係数によって計算した借入金総額は実際の金額とは異なり、概算となることに注意が必要です。
借入金総額の計算に年金現価係数が使える理由
住宅ローンなどの借金の借入金総額、いくらまで借りられるかを計算するために年金現価係数が利用できる理由は、住宅ローンなどの融資を貸している側から見ることによって理解できるようになります。
毎期(毎年)の受取金額は借り手にとっての毎年の返済金額、借入金利=融資金利で複利運用、毎期一定金額を受け取る(元利金の返済を受ける)、借入金総額=融資総額=融資の元本と考えると、将来の一定期間、毎期同額の希望する年金額を受け取る場合に必要となる現在時点での元本、という年金現価係数の定義に当てはまるためです。
年金現価係数の例題
(例題1)年率2%で複利運用しながら、毎年100万円の年金を20年間受け取りたい場合、必要な年金の原資はいくらになるか
利率2%、20年の年金現価係数は16.3514なので、100×16.3514=1635.14(万円)となります。
(例題2)年率2%、35年返済で毎年の返済額を150万円として住宅ローンを借りた場合、借入総額はいくらになるか?(毎年1回返済と仮定)
利率2%、35年の年金現価係数は24.9986なので、150×24.9986=3749.79(万円)となります。
年金現価係数の求め方・出し方
年金現価係数は年金現価係数表がある場合には、年金現価係数表から年金現価係数の値を探して求めます。年金現価係数表がない場合には、年金現価係数の計算式から年金現価係数を自分で計算によって算出する方法によって求めます。
年金現価係数を計算で算出する方法(計算式)
年金現価係数は年金現価係数表がある場合には年金現価係数表から値を求めます。年金現価係数表がない場合、年金現価係数表には載っていない場合には、次の年金現価係数の計算式から計算で求める方法もあります。年金現価係数の出し方は次の計算式に「r:利率(年間の運用利率)」と「n:期間(年)」を入力することによって算出することができます。
年金現価係数:{(1+r)n-1}/{r・(1+r)n}
年金現価係数の計算式の求め方
年金現価係数は、一定期間、一定利率で複利運用しながら、毎期一定の金額を取崩す場合に現在必要となる元本金額(年金原資)を求める係数です。
「r」を年間の運用利率、「n」を運用年数として、1年後、2年後、3年後、・・・・、n-1年後、n年後それぞれに取り崩される取崩時点での金額を、1/(1+r)n倍することによって現在の金額に換算し合計すれば、現在必要となる元本金額を求められることを利用して年金現価係数を求めます。
なお、取崩し(回収)は毎期末(年末)に行われるものとします。ここで「Fn」を期間n年の年金現価係数、「T」を毎年の取崩金額、「An」をn年目に取り崩した金額の複利運用前の現在時点での金額(利子を除いた元本に換算)、「Sn」を現在の元本金額(年金原資)とします。
年金現価係数の定義から以下の通りとなります。
T・Fn=Sn…(1)
1年後に取り崩した金額の複利運用前の現在時点での金額は、1年間年率r%で運用されていたため(1+r)で割ればよい(1/(1+r)をかければよい)ため、現在の金額に換算すると次のようになります。
1年後に取り崩した金額の現在換算金額:A1=T・{1/(1+r)1}
以下同様に次のようになります。
2年後に取り崩した金額の現在換算金額:A2=T・{1/(1+r)2}
3年後に取り崩した金額の現在換算金額:A3=T・{1/(1+r)3}
これをn-1年後、n年後まで立式すると次のような式になります。
n-1年後に取り崩した金額の現在換算金額:An-1=T・{1/(1+r)n-1}
n-2年後に取り崩した金額の現在換算金額:An=T・{1/(1+r)n}
ここで、1年後取崩金額からn年後取崩金額までの複利運用前の現在時点での金額に換算した額を合計すると現在の必要な元本金額(年金原資)となるため以下の式が成り立ちます。
Sn=A1+A2+A3+…+An-1+An
Sn=T・{1/(1+r)1}+T・{1/(1+r)2}+T・{1/(1+r)3}+…+T・{1/(1+r)n-1}+T・{1/(1+r)n}
Sn=T・{1/(1+r)}・{1+1/(1+r)+1/(1+r)2+…+1/(1+r)n-2+1/(1+r)n-1}
ここで2番目の中括弧{}内は初項1、公比1/(1+r)、項数nの等比数列であるため、等比数列の和の公式(a:初項、r:公比、n:項数)の次式より和を求めます。
等比数列の和の公式={a・(1-rn)}/(1-r)
Sn=T・{1/(1+r)}・[1-{1/(1+r)}n]/{1-1/(1+r)}
Sn=T・{1/(1+r)}・{1-1/(1+r)n}/{r/(1+r)}
Sn=T・{1/(1+r)}・[{(1+r)n-1}/(1+r)n]/{r/(1+r)}
Sn=T・{1/(1+r)}・[{(1+r)n-1}/{r・(1+r)n-1}]
Sn=T・{(1+r)n-1}/{r・(1+r)n}…(2)
(1)と(2)から以下の式を導きます。
Fn={(1+r)n-1}/{r・(1+r)n}
年金現価係数の覚え方
年金現価係数は、将来希望する一定金額の年金を毎期(毎年)を受け取るために必要な現在の元本(年金原資)を求めるので、(将来の)年金の現価(=現在必要な年金原資)の係数ということになります。年金とあるとおり(将来の)年金を受け取るための係数で、かつ、現価とあるとおり現在の金額を求める係数です。
年金現価係数に似た言葉として、年金終価係数がありますが、年金終価係数は年金に関する係数であるものの、この場合の年金は毎年同じ金額を積み立てるという意味で、毎年受け取るという意味ではありません。また、年金終価係数とあるとおり、将来の金額(積み立てた金額の元利金合計)に関する係数です。
年金現価係数と対をなすのは資本回収係数です。資本回収係数は、現在の元本(年金原資)は分かっていますが、毎年受け取る年金額が分からない場合に使います。年金現価係数は、毎年受け取る金額は分かっていますが、現在の元本(年金原資)が分からない場合に使います。
年金現価係数は、年金で年金受け取り、現価で現在の原資、というイメージを持つと覚えやすくなります。
年金現価係数を計算するエクセル関数
年金現価係数をエクセルで計算する場合には、PV関数を用います。PVは「Present Value」(現在価値)です。PV関数は(利率,期間,定期支払額,将来価値,支払期日)を入力します。
年金終価係数を計算したい場合、利率には複利運用する利率(例:1%なら0.01または1%)、期間には運用期間(例:5年なら5)、定期支払額は「-1」(負の結果になるためマイナスとし、毎期1を支払いと設定)、将来価値は「0」(最終時点で全て取り崩されてなくなるため)、支払期日は省略するか「0」(通常期末で算出します)と入力します。
年金現価係数表
年金現価係数表は以下の通りとなります。毎年希望する年金額を受け取るために必要な年金原資を計算するための表としても使えます。
| 期間 | 1% | 2% | 3% | 4% | 5% |
|---|---|---|---|---|---|
| 1 | 0.9901 | 0.9804 | 0.9709 | 0.9615 | 0.9524 |
| 2 | 1.9704 | 1.9416 | 1.9135 | 1.8861 | 1.8594 |
| 3 | 2.9410 | 2.8839 | 2.8286 | 2.7751 | 2.7232 |
| 4 | 3.9020 | 3.8077 | 3.7171 | 3.6299 | 3.5460 |
| 5 | 4.8534 | 4.7135 | 4.5797 | 4.4518 | 4.3295 |
| 6 | 5.7955 | 5.6014 | 5.4172 | 5.2421 | 5.0757 |
| 7 | 6.7282 | 6.4720 | 6.2303 | 6.0021 | 5.7864 |
| 8 | 7.6517 | 7.3255 | 7.0197 | 6.7327 | 6.4632 |
| 9 | 8.5660 | 8.1622 | 7.7861 | 7.4353 | 7.1078 |
| 10 | 9.4713 | 8.9826 | 8.5302 | 8.1109 | 7.7217 |
| 11 | 10.3676 | 9.7868 | 9.2526 | 8.7605 | 8.3064 |
| 12 | 11.2551 | 10.5753 | 9.9540 | 9.3851 | 8.8633 |
| 13 | 12.1337 | 11.3484 | 10.6350 | 9.9856 | 9.3936 |
| 14 | 13.0037 | 12.1062 | 11.2961 | 10.5631 | 9.8986 |
| 15 | 13.8651 | 12.8493 | 11.9379 | 11.1184 | 10.3797 |
| 16 | 14.7179 | 13.5777 | 12.5611 | 11.6523 | 10.8378 |
| 17 | 15.5623 | 14.2919 | 13.1661 | 12.1657 | 11.2741 |
| 18 | 16.3983 | 14.9920 | 13.7535 | 12.6593 | 11.6896 |
| 19 | 17.2260 | 15.6785 | 14.3238 | 13.1339 | 12.0853 |
| 20 | 18.0456 | 16.3514 | 14.8775 | 13.5903 | 12.4622 |
| 21 | 18.8570 | 17.0112 | 15.4150 | 14.0292 | 12.8212 |
| 22 | 19.6604 | 17.6580 | 15.9369 | 14.4511 | 13.1630 |
| 23 | 20.4558 | 18.2922 | 16.4436 | 14.8568 | 13.4886 |
| 24 | 21.2434 | 18.9139 | 16.9355 | 15.2470 | 13.7986 |
| 25 | 22.0232 | 19.5235 | 17.4131 | 15.6221 | 14.0939 |
| 26 | 22.7952 | 20.1210 | 17.8768 | 15.9828 | 14.3752 |
| 27 | 23.5596 | 20.7069 | 18.3270 | 16.3296 | 14.6430 |
| 28 | 24.3164 | 21.2813 | 18.7641 | 16.6631 | 14.8981 |
| 29 | 25.0658 | 21.8444 | 19.1885 | 16.9837 | 15.1411 |
| 30 | 25.8077 | 22.3965 | 19.6004 | 17.2920 | 15.3725 |
| 31 | 26.5423 | 22.9377 | 20.0004 | 17.5885 | 15.5928 |
| 32 | 27.2696 | 23.4683 | 20.3888 | 17.8736 | 15.8027 |
| 33 | 27.9897 | 23.9886 | 20.7658 | 18.1476 | 16.0025 |
| 34 | 28.7027 | 24.4986 | 21.1318 | 18.4112 | 16.1929 |
| 35 | 29.4086 | 24.9986 | 21.4872 | 18.6646 | 16.3742 |
| 36 | 30.1075 | 25.4888 | 21.8323 | 18.9083 | 16.5469 |
| 37 | 30.7995 | 25.9695 | 22.1672 | 19.1426 | 16.7113 |
| 38 | 31.4847 | 26.4406 | 22.4925 | 19.3679 | 16.8679 |
| 39 | 32.1630 | 26.9026 | 22.8082 | 19.5845 | 17.0170 |
| 40 | 32.8347 | 27.3555 | 23.1148 | 19.7928 | 17.1591 |
(注)期末に利子の処理を行う方式、小数第5位を四捨五入。
(出典)fromportal.comの担当者が作成
まとめ
- 年金現価係数は、将来の一定期間、希望する年金額を受け取る場合に必要となる現在時点での元本(年金原資)はいくらになるかを計算するために使う係数です。取崩ながら複利運用する場合に用いる係数です。
- 希望する毎期の受取金額(年金額)に年金現価係数をかけることで、現在必要となる元本金額(年金原資)を求めることができます。