年金終価係数とは(意味や定義・使い方・計算式・年金終価係数表)
記事作成日:2018年4月13日
年金終価係数とは、一定の期間、一定の金額を毎期同額で積み立てながら、一定の利率で複利運用した場合、将来いくらになるかを計算するための係数です。
年金終価係数の定義は「毎期の積立金額×年金終価係数=将来の積立金合計額」となることから、「年金終価係数=将来の積立金合計額÷毎期の積立金額」となります。つまり、年金終価係数とは最終的な積立金額(元利金合計)が毎期の積立金額の何倍になるかを示した係数です。毎期(通常は毎年)の積立金額に年金終価係数をかけることで、将来の積立金の合計額が分かります。
「年金終価係数」の読み方は「ねんきんしゅうかけいすう」です。年金終価係数の英語は「uniform series final worth factor」、「uniform series compound amount factor」などとなります。
また、「減債基金係数=毎期の積立金額÷将来の積立金合計額」であることから、年金終価係数は減債基金係数の逆数です。
スポンサーリンク
年金終価係数の図解
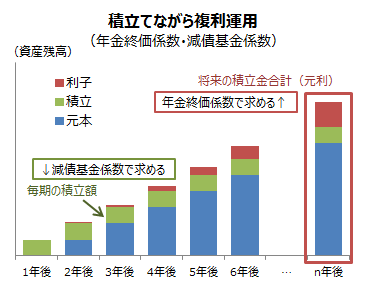
年金終価係数とは、積み立てながら複利運用した場合に、将来の積立金合計額(元利金合計)を求める係数です。毎期(通常は毎年)の積立金額に年金終価係数をかけることで将来の積立金合計額(元利金合計)を算出できます。
「年金」という言葉が含まれていますが、この年金には定期的に支払われるお金という意味がありますが、毎年の積み立てる金額に関するものということで、「年金終価係数」と年金がついていると考えるとイメージがしやすくなります。
年金終価係数の使い方・使用例
年金終価係数は「毎期の積立金額×年金終価係数=将来の積立金合計額」となるため、毎年一定金額を積み立てて複利運用した場合に最終的にいくらになるかを求めることができます。
例えば、積立預金・貯金を行う場合に最終的にはいくらになるか、給与天引きで預金をするような場合に最終的にいくらになるか、などの計算に用いることができます。他にもライフプランニングで、結婚資金、教育資金、住宅取得資金、介護資金、老後資金などを貯める場合に、毎月の積立金額から、いくら貯められるかなどの計算に使用します。
ただし、積立は1年に1回期末だけという訳ではなく通常は毎月行われるため、年単位で年金終価係数によって計算した将来の積立金額合計は実際の積立金額合計とは異なり、概算となります。
年金終価係数の例題
(例題1)毎年20万円を利率2%で積立預金をすると10年後にはいくらになるか?
利率2%、10年の年金終価係数は10.9497なので、20×10.9497=218.994(万円)となります。
(例題2)毎年100万円を積み立てながら利率3%で30年複利運用して老後資金を準備すると将来いくらになるか?
利率3%、30年の年金終価係数は47.5754なので、100×47.5754=4757.54(万円)となります。
年金終価係数の求め方・出し方
年金終価係数は年金終価係数表がある場合には、年金終価係数表から年金終価係数の値を探して求めます。年金終価係数表がない場合には、年金終価係数の計算式から年金終価係数を自分で計算によって算出する方法によって求めます。
年金終価係数を計算で算出する方法(計算式)
年金終価係数は年金終価係数表がある場合には年金終価係数表から値を求めます。年金終価係数表がない場合、年金終価係数表には載っていない場合には、次の年金終価係数の計算式から計算で求める方法もあります。年金終価係数の出し方は次の計算式に「r:利率(年間の運用利率)」と「n:期間(年)」を入力することによって算出することができます。
年金終価係数:{(1+r)n-1}/r
年金終価係数の計算式の求め方
年金終価係数は、毎期一定の金額を積み立てながら、一定期間、一定利率で複利運用した場合に将来の積立金合計額(元利)を求める係数です。
「r」を年間の運用利率、「n」を運用年数として、1年後、2年後、3年後、・・・・、n-1年後、n年後それぞれの積立金の運用後の元利金額を合計することによって将来の積立金合計額が求められることを利用して年金終価係数を求めます。
なお、積立は毎期末(年末)に行われるものとします。ここで「Fn」を期間n年の年金終価係数、「T」を毎年の積立金額、「An」をn年目に積立を開始したお金の複利運用後の最終的な金額(元利合計)、「Sn」をn年目の積立金合計額(元利)とします。
年金終価係数の定義から以下の通りとなります。
T・Fn=Sn…(1)
1年後に積立を開始したお金のn年までの複利運用後の金額はn-1年間年率r%で運用されるため(1+r)を(n-1)乗すればよいため、n年まで複利運用した結果は次の通りになります。
1年後積立開始分:A1=T・(1+r)n-1
以下同様に立式します。
2年後積立開始分:A2=T・(1+r)n-2
3年後積立開始分:A3=T・(1+r)n-3
これをn-1年後、n年後まで立式すると次のような式になります。
n-1年後積立開始分:An-1=T・(1+r)n-(n-1)=T・(1+r)1
n年後積立開始分:An=T・(1+r)n-n=T・(1+r)0
ここで、1年後積立開始分からn年後積立開始分までの複利運用後の金額を合計するとn年目の積立金合計額となるため以下の式が成り立ちます。
Sn=A1+A2+A3+…+An-1+An
Sn=T・(1+r)n-1+T・(1+r)n-2+T・(1+r)n-3+…+T・(1+r)+T
Sn=T・{(1+r)n-1+(1+r)n-2+(1+r)n-3+…+(1+r)+1}
ここで中括弧{}内は初項1、公比(1+r)、項数nの等比数列であるため、等比数列の和の公式(a:初項、r:公比、n:項数)の次式より和を求めます。
等比数列の和の公式={a・(1-rn)}/(1-r)
Sn=T・[1・{1-(1+r)n}/{1-(1+r)}]
Sn=T・[{(1+r)n-1}/r]…(2)
(1)と(2)から以下の式を導きます。
Fn={(1+r)n-1}/r
年金終価係数の覚え方
年金終価係数は年金に関する終価を求める係数となり、「年金=毎年の積立金」と考えると、毎年お金を積み立てた場合の最終的な積立金額という意味になります。毎年の積立金額を複利運用した場合の将来の積立金合計額を出すのが年金終価係数となります。
年金終価係数と対になる係数に減債基金係数がありますが、年金終価係数と減債基金係数はともに積み立てながら運用することは共通ですが、年金終価係数は最終的な積立金合計額を求める係数で、減債基金係数は毎期(毎年)の積立金額を求める係数です。
また、年金終価係数に似た言葉で年金現価係数がありますが、希望の年金額を受け取るために必要な「現在の」年金原資を求める係数です。
年金ということで毎年積立、終価ということで将来の金額と考えると、積立しながら複利運用した時の最終的な積立金合計額と覚えやすくなります。
年金終価係数を計算するエクセル関数
年金終価係数をエクセルで計算する場合には、FV関数を用います。FVは「Future Value」(将来価値)です。FV関数は(利率,期間,定期支払額,現在価値,支払期日)を入力します。
年金終価係数を計算したい場合、利率には複利運用する利率(例:1%なら0.01または1%)、期間には運用期間(例:5年なら5)、定期支払額は「-1」(負の結果となるためマイナスとし、毎期の積立金は1とする)、現在価値は「0」(最初は0から開始し毎期1を積立)、支払期日は省略するか「0」(通常期末で算出します)と入力します。
年金終価係数表
年金終価係数表は以下の通りとなります。毎年一定金額を複利運用で積立預金・積立貯金した場合の積立額(元利金合計)を計算するための表としても使えます。
| 期間 | 1% | 2% | 3% | 4% | 5% |
|---|---|---|---|---|---|
| 1 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| 2 | 2.0100 | 2.0200 | 2.0300 | 2.0400 | 2.0500 |
| 3 | 3.0301 | 3.0604 | 3.0909 | 3.1216 | 3.1525 |
| 4 | 4.0604 | 4.1216 | 4.1836 | 4.2465 | 4.3101 |
| 5 | 5.1010 | 5.2040 | 5.3091 | 5.4163 | 5.5256 |
| 6 | 6.1520 | 6.3081 | 6.4684 | 6.6330 | 6.8019 |
| 7 | 7.2135 | 7.4343 | 7.6625 | 7.8983 | 8.1420 |
| 8 | 8.2857 | 8.5830 | 8.8923 | 9.2142 | 9.5491 |
| 9 | 9.3685 | 9.7546 | 10.1591 | 10.5828 | 11.0266 |
| 10 | 10.4622 | 10.9497 | 11.4639 | 12.0061 | 12.5779 |
| 11 | 11.5668 | 12.1687 | 12.8078 | 13.4864 | 14.2068 |
| 12 | 12.6825 | 13.4121 | 14.1920 | 15.0258 | 15.9171 |
| 13 | 13.8093 | 14.6803 | 15.6178 | 16.6268 | 17.7130 |
| 14 | 14.9474 | 15.9739 | 17.0863 | 18.2919 | 19.5986 |
| 15 | 16.0969 | 17.2934 | 18.5989 | 20.0236 | 21.5786 |
| 16 | 17.2579 | 18.6393 | 20.1569 | 21.8245 | 23.6575 |
| 17 | 18.4304 | 20.0121 | 21.7616 | 23.6975 | 25.8404 |
| 18 | 19.6147 | 21.4123 | 23.4144 | 25.6454 | 28.1324 |
| 19 | 20.8109 | 22.8406 | 25.1169 | 27.6712 | 30.5390 |
| 20 | 22.0190 | 24.2974 | 26.8704 | 29.7781 | 33.0660 |
| 21 | 23.2392 | 25.7833 | 28.6765 | 31.9692 | 35.7193 |
| 22 | 24.4716 | 27.2990 | 30.5368 | 34.2480 | 38.5052 |
| 23 | 25.7163 | 28.8450 | 32.4529 | 36.6179 | 41.4305 |
| 24 | 26.9735 | 30.4219 | 34.4265 | 39.0826 | 44.5020 |
| 25 | 28.2432 | 32.0303 | 36.4593 | 41.6459 | 47.7271 |
| 26 | 29.5256 | 33.6709 | 38.5530 | 44.3117 | 51.1135 |
| 27 | 30.8209 | 35.3443 | 40.7096 | 47.0842 | 54.6691 |
| 28 | 32.1291 | 37.0512 | 42.9309 | 49.9676 | 58.4026 |
| 29 | 33.4504 | 38.7922 | 45.2189 | 52.9663 | 62.3227 |
| 30 | 34.7849 | 40.5681 | 47.5754 | 56.0849 | 66.4388 |
| 31 | 36.1327 | 42.3794 | 50.0027 | 59.3283 | 70.7608 |
| 32 | 37.4941 | 44.2270 | 52.5028 | 62.7015 | 75.2988 |
| 33 | 38.8690 | 46.1116 | 55.0778 | 66.2095 | 80.0638 |
| 34 | 40.2577 | 48.0338 | 57.7302 | 69.8579 | 85.0670 |
| 35 | 41.6603 | 49.9945 | 60.4621 | 73.6522 | 90.3203 |
| 36 | 43.0769 | 51.9944 | 63.2759 | 77.5983 | 95.8363 |
| 37 | 44.5076 | 54.0343 | 66.1742 | 81.7022 | 101.6281 |
| 38 | 45.9527 | 56.1149 | 69.1594 | 85.9703 | 107.7095 |
| 39 | 47.4123 | 58.2372 | 72.2342 | 90.4091 | 114.0950 |
| 40 | 48.8864 | 60.4020 | 75.4013 | 95.0255 | 120.7998 |
(注)期末に利子の処理を行う方式、小数第5位を四捨五入。
(出典)fromportal.comの担当者が作成
まとめ
- 年金終価係数は、一定期間、一定金額を毎期同額で積み立てながら一定利率で複利運用した場合、将来いくらになるかを計算するために使う係数です。
- 毎期の積立金額に年金終価係数をかけることで、将来の積立金合計額(元利金合計)を求めることができます。